主页 > 生活 >
方法 1化简完全平方数的平方根

1
背诵一些完全平方数和它们的平方根。将一个数平方,或者将它自身相乘,你就可以得到一个完全平方数。举例来说, 25是一个完全平方数,因为5×5或52等于25 。至少得记住1到10的完全平方数,那样可以帮助你识别并迅速化简完全平方根。以下是1到10的完全平方数:
- 12 = 1
- 22 = 4
- 32 = 9
- 42 = 16
- 52 = 25
- 62 = 36
- 72 = 49
- 82 = 64
- 92 = 81
- 102 = 100

2
找出一个完全平方数的平方根。如果你根号下看到一个完全平方数,你只需要去掉根号( √ ),并写下完全平方数的平方根。如果你已经记住了,那么就大功告成了。如果数目太大,你不知道,且该数是一个完全平方数,只要尝试用计算器对一个差不多的整数进行平方,你就会很快得到答案。例如,如果你看到根号下面是25,那么你就知道答案是5,因为25是一个完全平方数。
方法 2通过因数法化简平方根

1
如果该数字是偶数,除以2。寻找一个数的因数意味着寻找一切可以通过相乘得到该数字的数字,它可以帮助你化简平方根。如果该数字是偶数,那么你可以做的第一件事就是除以2。在这个例子中, √98变成√(2x49),因为98除以2为49。如果你的数字不能被2整除,尝试3,4,5,依此类推,直到你得到一个因数。
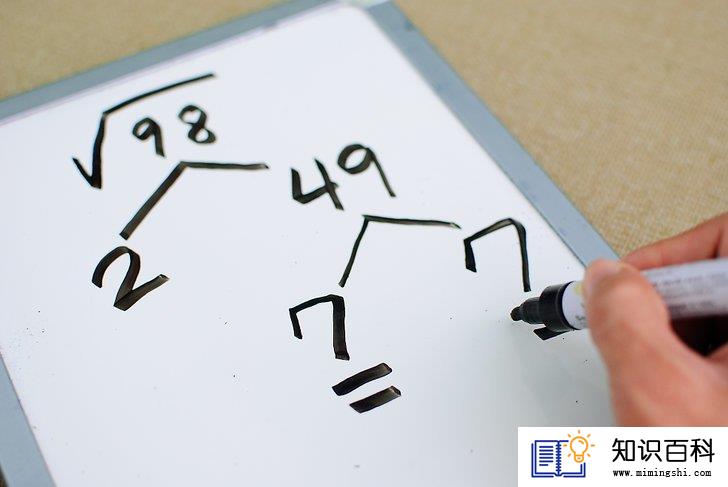
2
通过寻找因数来找到该数的完全平方数因数。看看你是否可以继续将它分解为因数的乘积。 2是素数,只能被1和它本身整除,所以你不能找到另一个因数。不过对于49,仍然存在其他因数,49可以细分为7×7,它正好是一个完全平方数。所以,你可以将√(2x49)分解为√(2x7x7),或√[2(72)],这意味着我们找到了期待的完全平方数。

3
化简平方根。因为√98=√[2(72)],所以你可以把一个7拿到根号外,将其化简为√98 = 7√2。你可以认为这是“非平方”的一个数,如果你能将一个数拿到根号外。所以,√49,或者是√(7 x 7),当你将它拿出根号之后它就变成7。如果你从根号外把7拿到里面,那么它就会被平方,变为49。因此,√98 = 7√2。
- 因此,对√[2(72)],√72变成位于√左侧的7,以及根号里面的2。
方法 3其它化简平方根的策略

1
要知道,开方符号(√)是开平方。例如,在这个问题,√25中,“√”是开方符号的象征。

2
开方是针对根号内的数字,你需要找到这个数字的平方根。例如,在√25的问题中, “25”是被开方数。

3
系数是根号外的倍数。这是平方根相乘的数;位于√的左边。例如,在该问题,7√2中,“7”是系数。

4
一个因数是可以整除另一个数的数。例如,2是8的因数,因为8 ÷4 = 2,但3不是8的因数,因为8÷3不能得到一个整数。例如,5是25的因数,因为5×5 = 25。

5
理解化简平方根的含义。化简平方根意味着分解出完全平方数,将它们转移到根号的左边,在根号内留下其他因数。如果数字是一个完全平方数,写出根后,根号就会消失。例如,√98可以化简为7√2。
小提示
- 找到完全平方数的方法之一是去翻完全平方数列表,从接近开方数的下一个最小的数开始。例如,寻找27的完全平方根时,可以从25开始,找到16,最后停在9,它可以被27整除。
警告
- 除了要决定完全平方数在开方数中有多少次以外,不建议使用计算器。
- 化简与求值不同。在化简过程中,绝对不能出现任何小数。
