主页 > 生活 >
方法 1通过边长和边心距求面积

1
从边长和边心距入手。这个方法适用于求五个内角大小完全相等的正五边形面积。除了边长信息,你还得知道五边形的“边心距”。边心距是五边形每条边到其外接圆的圆心的距离,从圆心到边作垂线,垂线与五边形的边形成的夹角正好是90º。
- 不要混淆边心距和半径的概念,半径是从中心到五边形边角(顶点),而边心距则是中心到五边形的边中点的距离。如果你只知道边长和半径长,请跳至第二种方法。
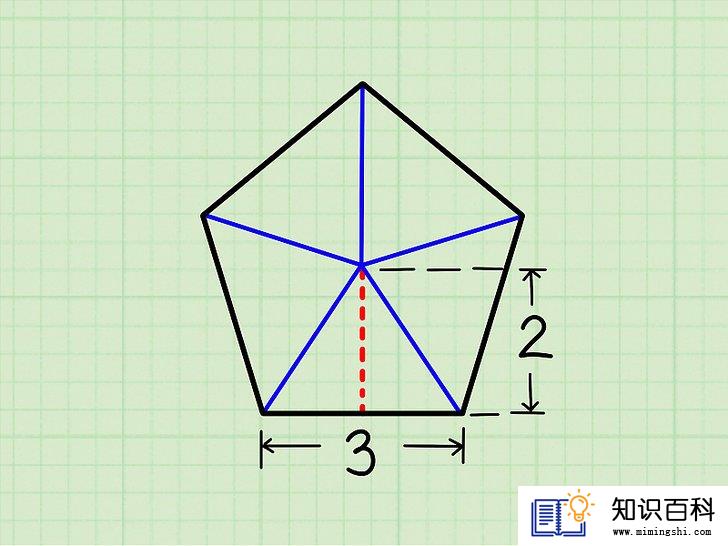
- 我们将以边长为3个单位长度和边心距为2个单位长度的五边形为例。
2
将五边形分割成五个三角形。从外接圆圆心向五边形的边角(顶点)画五条直线,这样能将其分割成五个三角形。

3
计算三角形的面积。每个三角形都有一个底边,长度等于五边形的边长。三角形也有一个 高,长度和五边形的边心距相等。(记住,三角形的高是从一个顶点向对边作垂线,形成一个直角)。计算三角形面积的公式是:面积S=½ x 底边长 x 高。
- 在我们的示例中,三角形面积 = ½ x 3 x 2 = 3 单位面积。

4
用三角形面积乘以5,求出五边形面积。我们将五边形等分为五个三角形,每个三角形面积相等,五边形的面积就是三角形的面积乘以5。
- 在我们的例子中,A(五边形面积) = 5 x A(三角形面积)= 5 x 3 = 15 单位面积。
方法 2通过边长求面积
1
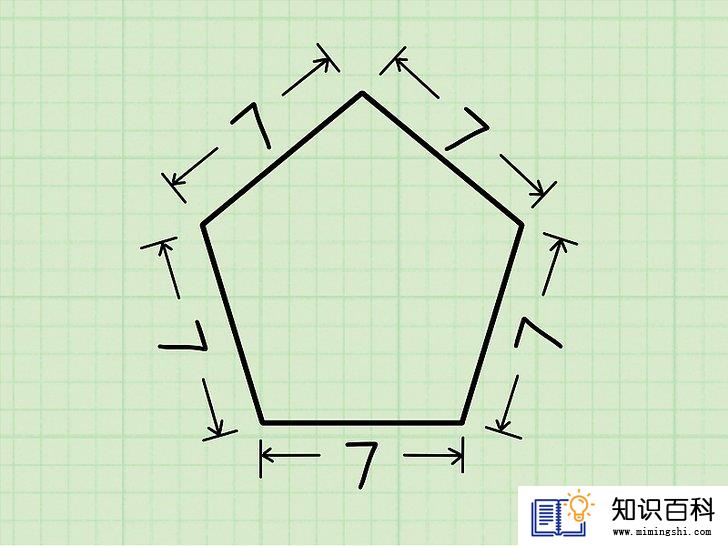
仅从边长入手。这个方法适用于求五条边长完全相等的正五边形面积。
- 在这一部分,我们使用边长为7个单位长的五边形为例。

2
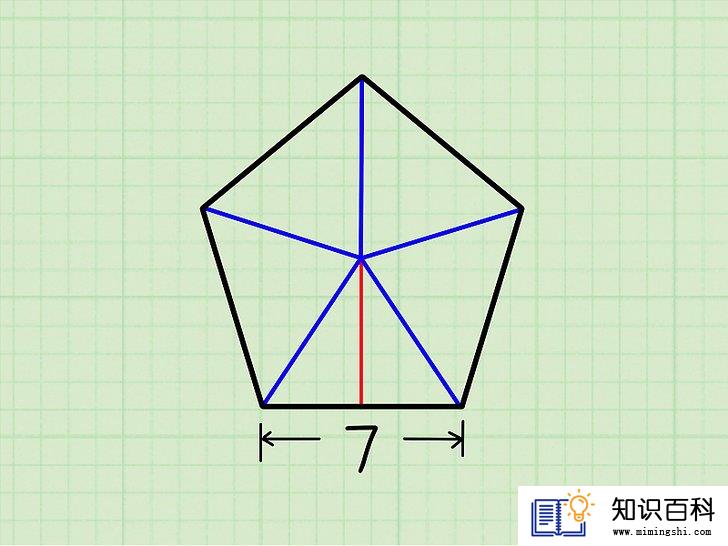
将五边形分割成五个三角形。从外接圆圆心向五边形的五个边角(顶点)画线,这样就把五边形分割成了五个大小相等的三角形。
3
将三角形分成两半。从五边形的中点向三角形底边作垂线,这条线和底边相交形成90º角,并将三角形分成两半,形成两个更小的三角形。
4
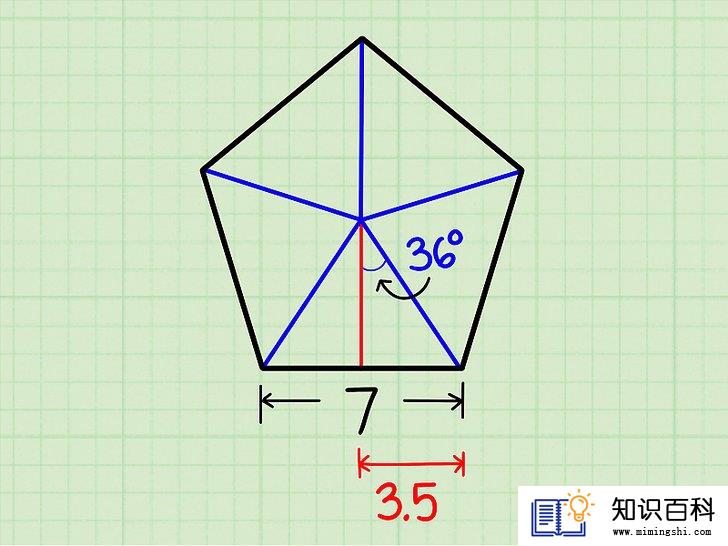
标记小三角形的已知信息。我们已经知道了小三角形的一边和一个角:
- 三角形的底边 就是五边形边长的 ½ 。在本例中,小三角形的底边为½ x 7 = 3.5 单位长。
- 三角形的顶角 等于大三角形顶角的一半,也就是36º 。(具体计算过程是:中心是360º,我们将其分为10个相同的小三角形,也就是360 ÷ 10 = 36。所以顶角为36º)。

5
计算三角形的高。三角形的高就是从五边形中心向边作的垂线,形成一个直角。我们可以使用三角函数来求出高的长度:
- 在直角三角形中,一个角的正切函数 等于对边长除以临边长。
- 36º角的对边是三角形的底(五边形边长的一半)。36º 角的临边是三角形的高。
- tan(36º) = 对边/ 临边
- 在本例中,tan(36º) = 3.5 / 高
- 高 x tan(36º) = 3.5
- 高= 3.5 / tan(36º)
- 高= (约等于) 4.8 单位长。

6
计算三角形的面积。三角形的面积等于½ x底边长x高(A = ½bh)。此时我们已知高和底边,代入公式即可求出三角形面积。
- 在本例中,小三角形的面积 = ½bh = ½(3.5)(4.8) = 8.4 单位面积。

7
乘以数量求出五边形面积。一个小三角形的面积是五边形面积的1/10。所以,要求五边形面积,用小三角形面积乘以10即可。
- 在本例中,五边形面积 = 8.4 x 10 = 84 单位面积。
方法 3使用公式
1
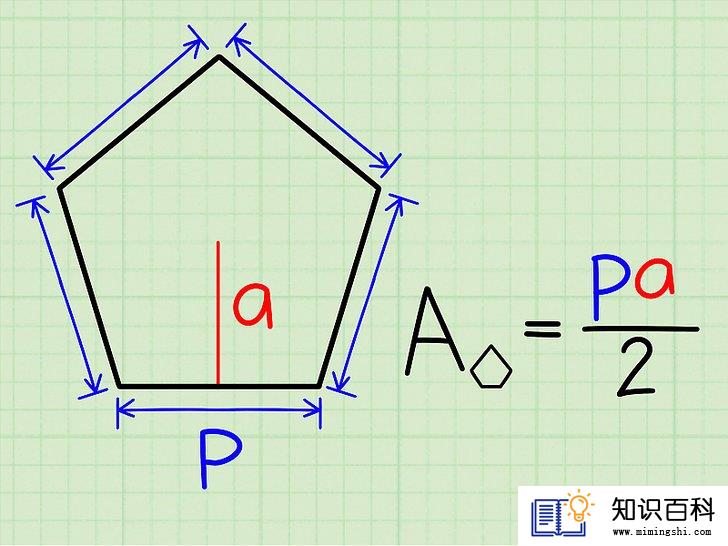
使用周长和边心距来计算面积。边心距是从五边形中心向边作垂线,垂线的长度就是边心距大小。如果已经知道这个长度,你可以使用下面这个简单的公式。
- 正五边形的面积= “pa”/2,其中“p” = 周长,“a” = 边心距。
- 如果不知道周长,可以通过边长来计算。计算公式是:p = 5s,其中“s”是边长。
2
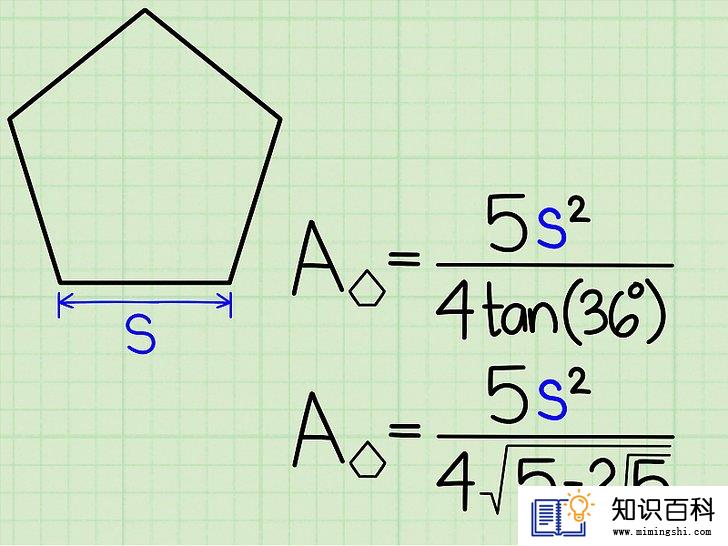
使用边长来计算面积。如果你只知道边长,那么使用以下公式进行计算:
- 正五边形的面积 = (5s2) / (4tan(36º)),其中“s” = 边长。
- tan(36º) = √(5-2√5) 。如果你的计算器没有“tan”功能,可以使用面积公式:面积 = (5s2) / (4√(5-2√5))。

3
选择只用半径来求面积的公式。如果你只知道半径,也可以求面积。使用以下公式:
- 正五边形的面积 = (5/2)r2sin(72º),其中“r”是半径。
小提示
- 不规则的五边形,即五条边不相等的五边形,其面积是比较难计算的。最好的计算方法将五边形分割成几个三角形,然后将它们的面积加起来。你还可以用规则的形状将五边形包围起来,然后通过减去多余部分的面积,就可以得到五边形的面积了。
- 同时使用几何法和公式法,比较之后确定正确的答案。如果你将数据一次全带入公式进行计算,得到的结果可能会有一点不同(因为中间过程不需要求近似),但是它们应该很接近。
- 例子里用的结果是近似值,是为了方便计算。如果你要计算给定边长的五边形的面积,那么不同的边长得到的面积也不同。
- 公式法可以由几何方法推导出来,推导过程和文中描述的类似。你可以尝试推导一下。通过半径求五边形面积的方法是比较难推导的(小提示:你可能需要用到二倍角等式)。
- 上一篇:如何求两点之间的距离
- 下一篇:如何求出一组数的众数
