主页 > 生活 >
方法 1正方形、矩形和其他平行四边形
1
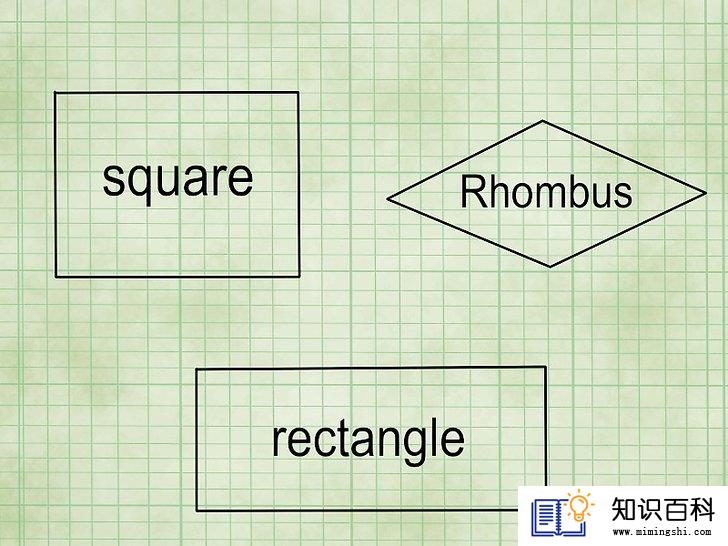
知道如何识别平行四边形。平行四边形是由两组平行线段组成的四边形,其对边长度相等。平行四边形包括:
- 正方形:四条边,长度相等。四个角均为90度直角。
- 矩形:四条边,对边长度相等。四个角均为90度。
- 菱形:四条边,长度相等。四个角,没有任何角等于90度,但对角必须相等。
2
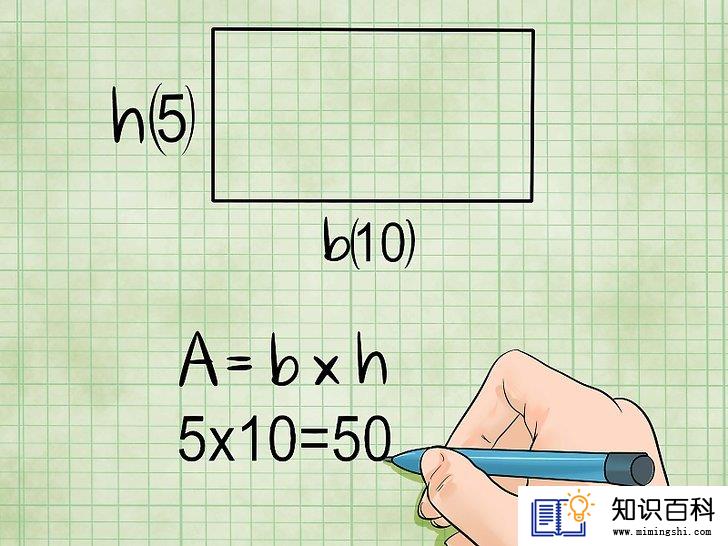
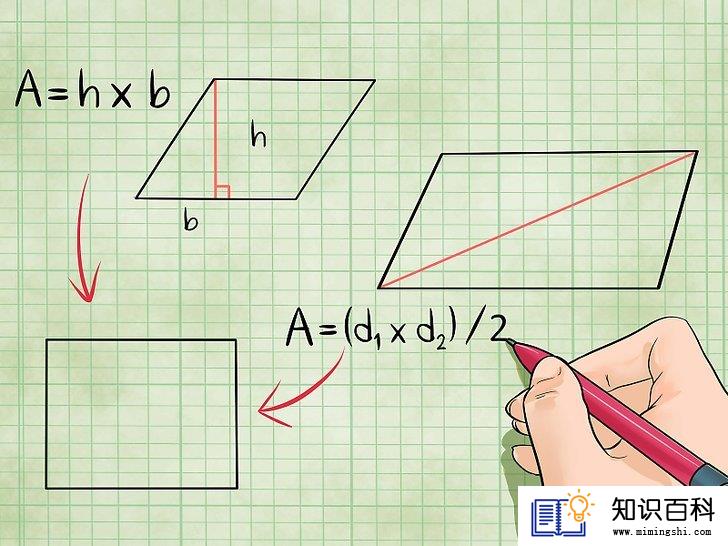
矩形的面积等于底乘以高。要计算矩形的面积,你需要知道两个数值:宽或底,以及长或高。前者是矩形较长的边,而后者是较短的边。然后,只需要将它们相乘,就能算出矩形的面积。换而言之:
- 面积 = 底 × 高,或简写为A = b × h。
- 示例:如果矩形的底长为10厘米,高为5厘米,则矩形的面积为10 × 5(b × h)= 50平方厘米。
- 求形状的面积时,不要忘了给答案加上合适的单位,比如“平方单位”,如平方毫米、平方厘米、平方米等。

3
正方形的面积等于边长的平方。从根本上来说,正方形是一种特殊的矩形,所以你可以使用相同的公式来求正方形的面积。但是,由于正方形各边的边长相等,所以可以简单记为边长的平方。这实际上就是在用正方形的底乘以高,因为底和高相等。使用如下公式:
- 面积 = 边长 × 边长,即A = s2
- 示例:如果正方形的边长为4厘米,即t = 4,则该正方形的面积为t2,或4 x 4 = 16平方厘米。
4
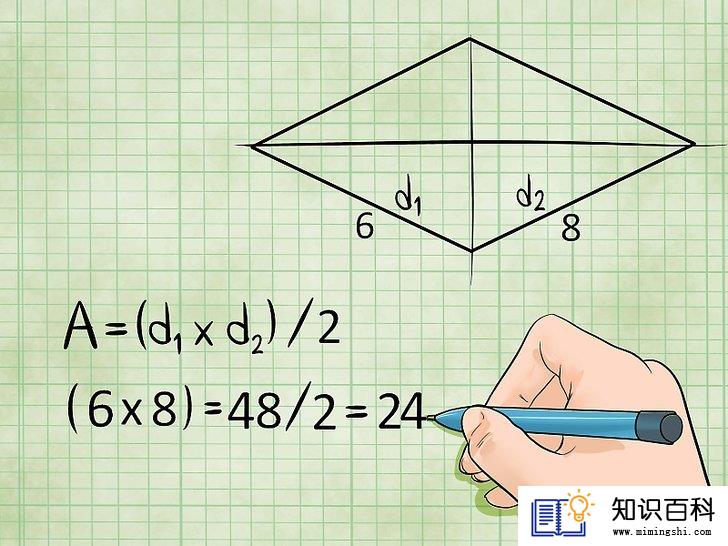
菱形的面积等于对角线相乘,再除以2。这里要注意了,在求菱形面积时,不能简单地用两条邻边边长相乘。你应该求出对角线长度,即连接各组对角线段的长度,用两者相乘,然后除以二。换而言之:
- 面积 = (对角线1 × 对角线2)/2,即A = (d1 × d2)/2
- 示例:如果一个菱形的对角线长度为6米和8米,则面积为(6 × 8)/2 = 48/2 = 24平方米。
5
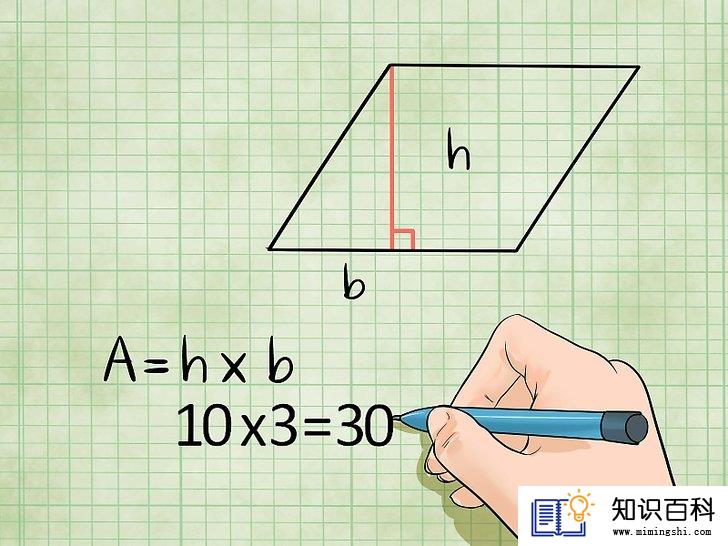
还可以用底×高来求菱形的面积。严格来说,你还可以使用底乘以高的公式来求菱形的面积。但是,其中“底”和“高”并不等于两条邻边的边长。首先,选一条边做底。然后,从底边向对边画一条线。这条线与两条边应该成90度,这个长度就是你应该使用的高。
- 示例:菱形的边长为10公里和5公里。两条10公里长的边之间的垂线长度为3公里。如果你想求菱形的面积,可以用10 × 3 = 30平方公里。
6
注意,菱形和矩形的公式适用于正方形。用上述的边长×边长公式来求正方形面积要方便得多。但由于正方形严格来说也是矩形和菱形,因此它们的面积公式同样也适用于计算正方形的面积。换而言之,就正方形而言:
- 面积 = 底 × 高,或A = b × h
- 面积 = (对角线1 × 对角线2)/2,或A = (d1 × d2)/2
- 示例:一个四边形两条邻边的长度均为4米。求这个正方形的面积时,可以用它的底乘以高:4 × 4 = 16平方米。
- 示例:一个正方形的两条对角线长度都等于10厘米。你可以用对角线公式来求这个正方形的面积:(10 × 10)/2 = 100/2 = 50 平方厘米。
方法 2求梯形的面积

1
知道如何识别梯形。梯形是至少有两条边平行的四边形。内角可以为任意度数。梯形的四条边长度可以各不相同。
- 求梯形的面积时,你可以使用两种不同的方法,具体取决于你手上掌握的信息。这里我们会对两种方法进行讲解。
2
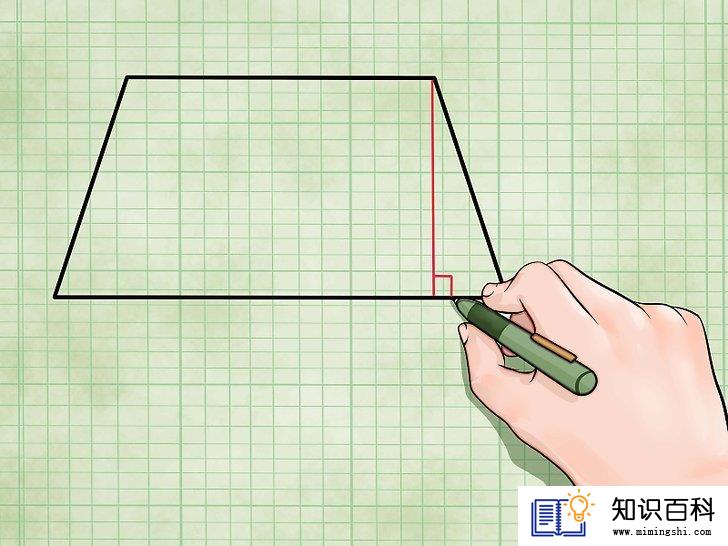
求梯形的高。梯形的高是连接两条平行边的垂直线段。它通常“不”等于一条边的边长,因为各边通常不会彼此垂直。两个面积公式都会用到梯形的高。以下是求梯形高的方法:
- 找到两条底线(即平行边)中较短的那条。以该底线与一个非平行边的交点为起点。画一条垂直于两条底线的线段。测量该线段的长度,即得到梯形的高。
- 如果高度线、底边和另一边构成一个直角三角形,你有时也可以用三角学来确定高度。更多信息可以参考网上关于三角学的文章。
3
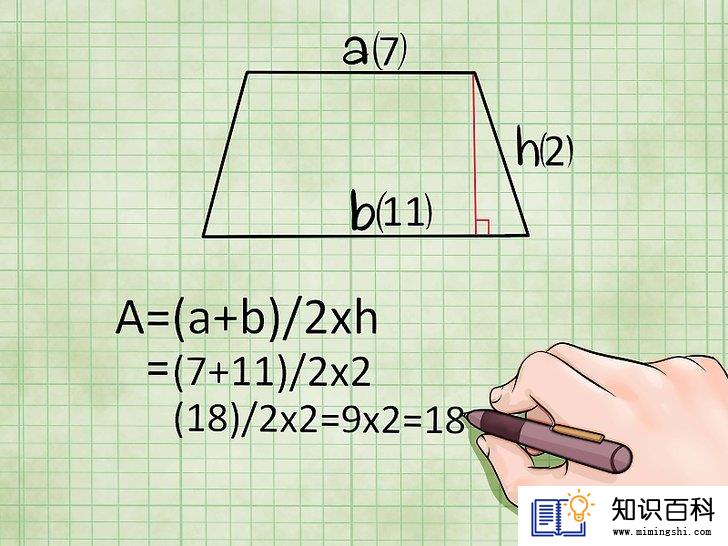
用高度和两条底边的长度来求梯形的面积。如果你知道梯形的高度,以及两条底边的长度,可以使用以下公式:
- 面积 = (底1 + 底2)/2 × 高,即A = (a+b)/2 × h
- 示例:如果一个梯形的一条底边长7米,另一条底边长11米,且连接两边的高长2米,则面积计算过程如下:(7 + 11)/2 × 2 = (18)/2 × 2 = 9 × 2 = 18平方米。
- 如果高等于10,而两条底边长度分别为7和9,进行如下计算可求出其面积:(7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80

4
用两条边的中线段来求梯形面积。中线段是平行于梯形底边和顶边的假想线,与两边的距离完全相等。由于中线段“总是等于(底1 + 底2)/2”,如果你知道它的长度,可以将梯形公式简化为:
- 面积 = 中线段 × 高,即A = m × h
- 从根本上说,这种计算方法使用的仍然是原始公式,只不过使用“m”代替了(a + b)/2。
- 示例:以上示例中,梯形的中线段长度为9米。这意味着我们可以用9 × 2 = 18平方米来计算梯形的面积,所得结果与之前的一样。
方法 3求对称四边形的面积

1
知道如何识别对称四边形。对称四边形是两对“邻边”长度相等,“而非对边”长度相等的四边形。顾名思义,对称四边形沿中线对称。
- 求对称四边形的面积时,可以使用两种不同的方法,具体取决于你手上掌握的信息。这里我们会对两种方法进行讲解。
2
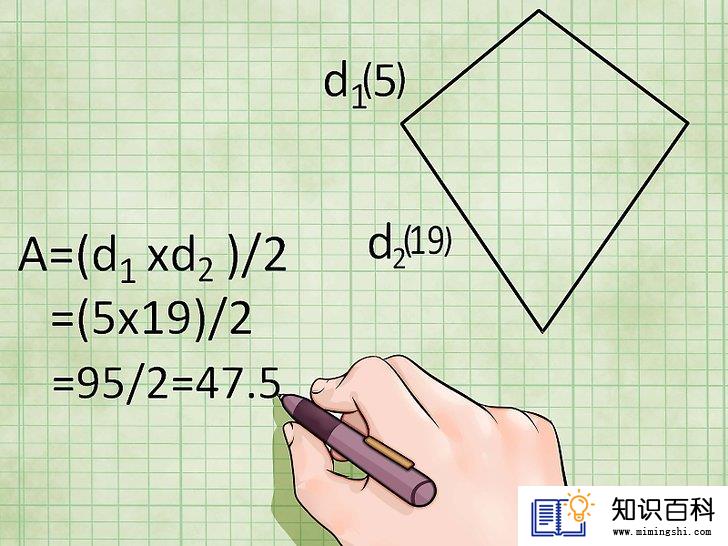
使用菱形对角线公式来求对称四边形的面积。菱形是各边长度相等的特殊对称四边形,因此你也可以使用对角线菱形面积公式,求出对称四边形的面积。对角线是连接对称四边形对角的直线。和菱形一样,对称四边形面积公式是:
- 面积 = (对角线1 × 对角线2)/2,即A = (d1 × d2)/2
- 示例:如果一个对称四边形的对角线长度为19米和5米,则其面积为(19 × 5)/2 = 95/2 = 47.5平方米。
- 如果你不知道对角线的长度,而且无法测量,可以使用三角学来进行计算。更多信息参见《计算对称四边形面积》一文。
3
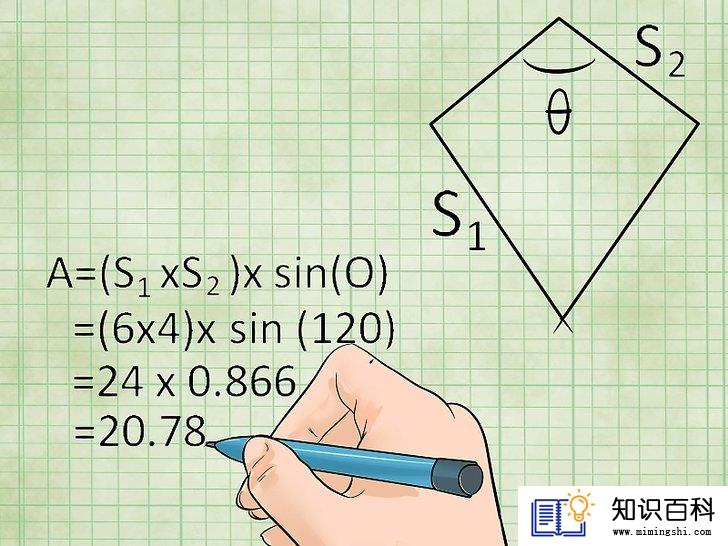
利用边长和各边的夹角来求面积。如果你知道两个不同的边长及各边之间的夹角,可以使用三角学原理求出对称四边形的面积。使用这一方法,你必须知道如何解正弦函数,或至少有一个可以解正弦函数的计算器。更多信息可以参考网上关于三角学的文章,或使用以下公式:
- 面积 = (边1 × 边2) × sin (角),即A = (s1 × s2) × sin(θ),其中θ是边1和边2之间的夹角。
- 示例:你有一个对称四边形,两组边长分别为6米和4米。其夹角约为120度。这种情况下,你可以求出其面积,具体如下:(6 × 4) × sin(120) = 24 × 0.866 = 20.78平方米
- 注意,公式中使用的是两个“不同的”边长和它们之间的夹角,而不能使用一组相同长度的邻边。
方法 4求任意四边形的面积

1
求所有四边形的面积。你遇到的四边形可能不属于以上任何一类,例如,它四条边的长度可能各不相同,而且没有任何对边互相平行。有多个公式可以用来计算任意四边形的面积,而无论其形状。本节会介绍其中最常用的一种公式。注意,该公式要用到三角学知识。更多信息可以参考网上关于基本三角学的文章。
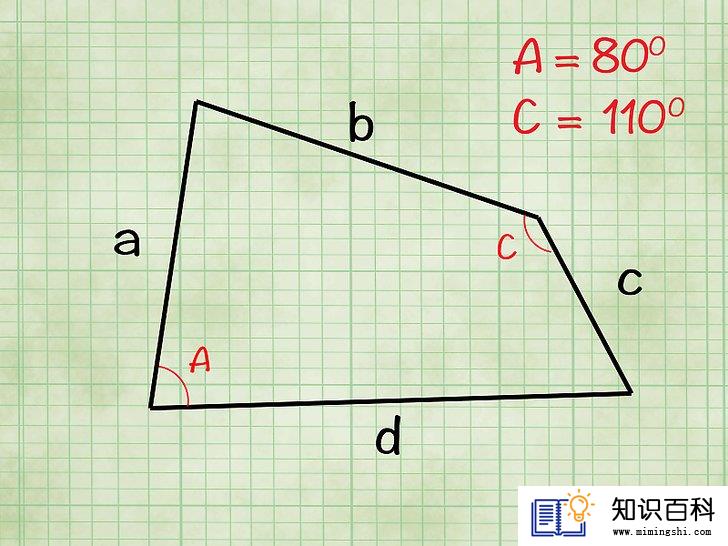
- 首先,你必须知道四边形四条边的边长。为了方便本文讲解,我们用a、b、c、d来指代它们。边a和边c为对边,而边b和边d为对边。
- 示例:如果你有一个不属于上述任何类别的不规则四边形,先测量其各边长度。假设边长分别为12厘米、9厘米、5厘米和14厘米。在以下步骤中,你会用到这些信息来求四边形的面积。
2
求得各边之间夹角的角度。计算不规则四边形的面积时,只知道边长是不够的。继续求得两个对角的角度。为了方便本节讲解,我们会用“角A”来指代边a和边d之间的夹角,用“角C”来指代边b和边c之间的夹角。不过,你也可以使用另外一组对角。
- 示例:假设在该四边形中,角A等于80度,而角C等于110度。在下一步中,你会用到这些值来求四边形的总面积。

3
使用三角形面积公式来求四边形的面积。想象边a和边b的夹角到边c和边d的夹角之间有一条直线。这条线会将四边形分割成两个三角形。由于三角形的面积等于absinC,其中“C”为边a和边b的夹角,你可以两次使用这一公式,分别求出被分割成的两个三角形的面积,来算出四边形的总面积。换而言之,对任意四边形而言:
- 面积 = 0.5 边1 × 边4 × sin(边1&4角) + 0.5 × 边2 × 边3 × sin (边2&3角),即
- 面积 = 0.5 a × d × sin A + 0.5 × b × c × sin C
- 示例:你已经知道所需的边长和角度值,因此计算过程如下:
- = 0.5 (12 × 14) × sin (80) + 0.5 × (9 × 5) × sin (110)
- = 84 × sin (80) + 22.5 × sin (110)
- = 84 × 0.984 + 22.5 × 0.939
- = 82.66 + 21.13 = 103.79平方厘米
- 注意,如果你想求对角相等的平行四边形的面积,公式可以简化为面积 = 0.5*(ad + bc) * sin A。
小提示
- 使用三角形计算器可以帮助上述“任意四边形”方法中的计算。
- 更多信息可以参考wikiHow关于特殊形状面积的文章:如何计算正方形的面积,如何计算矩形的面积,如何计算菱形的面积,如何计算梯形的面积,以及如何计算对称四边形的面积
- 上一篇:如何求3X3矩阵的行列式
- 下一篇:没有了
- 02-05橄榄皮是不是见光就白
- 01-19如何煮荷包蛋
- 02-06如何求3X3矩阵的行列式
- 01-23如何和顽固的人打交道
- 01-19如何制作香蕉片
- 01-16如何改善记忆力
- 01-19如何用种子种植番茄
- 01-18如何防止住宅火患
- 02-06如何用APA格式引用年度报告
- 01-23如何结束短信聊天
- 01-18如何集中注意力学习
- 01-16如何有效地学习
- 01-16如何提高学习速度
- 01-16如何成为知识渊博的人
- 01-16如何学习基本英语
